c言語で微分方程式を解く（修正オイラー法）

前回の記事では微分方程式を解く方法として、オイラー法を紹介しましたが、さらに精度の良い方法として修正オイラー法があるので今回はそれについて書きたいと思います。
前回の記事は、以下のリンクよりアクセスできるので、気になる方はご覧ください。

さらに精度よく計算できるルンゲクッタ法の記事を書きました。
c言語で微分方程式を解く（ルンゲクッタ法） - pypy.com/

修正オイラー法の考え方
実際にコードを書いてみる

修正オイラー法の考え方

前回と同じように、
$\frac{dy}{dx} = f(x,y) \tag{1}$
について考えます。

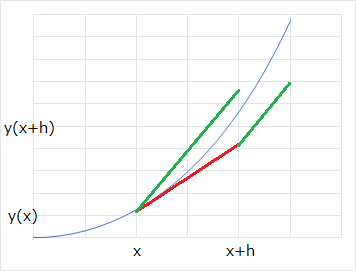
上図について、赤線の傾きは(1)式より、 $f(x,y)$ となります。
ここまでは、オイラー法と同様で、修正オイラー法になると増えるのは緑線の傾きです。
赤線の傾きが $f(x,y)$ であるから、 $x=x+h$ での $y$ の値は
\begin{align}　
y(x+h)=y(x)+hf(x,y)
\end{align}　
と書くことができます。
ここで、 $k_1=hf(x,y)$ とすると、
$y(x+h)=y(x)+k_1 \tag{2}$
となります。
(2)式をもとにすると、 $x=x+h$ における傾き（緑線の傾き）は、
\begin{align}　
f(x+h,y(x)+k_1)
\end{align}　
この緑線の傾きをもとに、 $x=x+h$ の $y$ の値を計算すると、
\begin{align}　
y(x+h)=y(x)+hf(x+h,y(x)+k_1)
\end{align}　
ここで、 $k_2=hf(x+h,y(x)+k_1)$ とすると
$y(x+h)=y(x)+k_2 \tag{3}$
上の図のように、一般的には、求めたい値は赤線と緑線の間に存在するため、
修正オイラー法では、
$y(x+h)=y(x)+ \frac{1}{2}(k_1+k_2) \tag{4}$
とします。
これを続けることで、(1)式の解を得ることができます。

実際にコードを書いてみる

それでは、コードを書いていきます。
今回は、前回のオイラー法と同じように、
\begin{align}　
\frac{dy}{dx} = xy　\tag{5}
\end{align}
を初期値 $(x_0,y_0)=(0.0,4.0)$
分割数100で解きたいと思います。
なお、(5)式の厳密解は
\begin{align}　
y = 4e^ \frac{x^2}{2}　
\end{align}
です。
厳密解との比較もしたいと思います

#include <stdio.h>
#include <math.h>

#define N 100 //分割数

double f(double x,double y);
double y_true(double x);

int main(void){
  //初期値
  double x=0.0;
  double y=4.0;
  double h=(3.0-0.0)/(double)N; //刻み幅

  printf("x       y       y_true\n");
  for(double i=0; i<N; i++){
    double k1 = h*f(x,y);
    double k2 = h*f(x+h,y+k1);
    y = y + (k1+k2)/2.0;
    x = x + h;
    printf("%5.5lf, %5.5lf, %5.5lf\n",x,y,y_true(x));
  }
}

double f(double x,double y){
  return x*y;
}
double y_true(double x){
  return 4.0*exp(x*x/2.0);
}

出た値をグラフにしてみると以下のようになります。

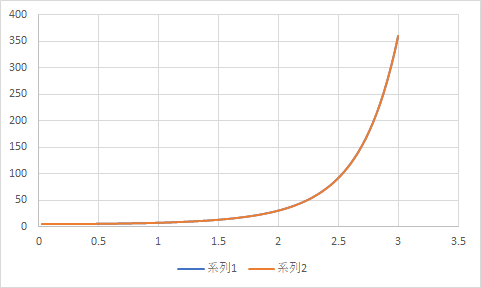
見るとわかるように、グラフがほとんど重なっており、精度がオイラー法より良くなったことがわかります。
実際に $x=3.0$ の時の値を見ると厳密解が 360.06853 で求めた値が 359.03017 であるため、そこまでの精度を求めない場合には充分であると思います。
今回は以上で終わります。