こんにちは。
今回はPythonで微分方程式を解くということで、オイラー法をやっていきます。
オイラー法の考え方
オイラー法の考え方について、詳しくは以下の記事で紹介しているので、参考にしてください。
taiboman.com
ここでは、簡単に説明します。
以下のような、微分方程式について考えます。
この式の解をとして、
まわりで、テイラー展開をすると、
となり、これを繰り返して解を求めます。
オイラー法のコード(Python)
それでは、コードを書きます。
今回は以下の式を、以下の初期値で解きます。
なお、厳密解は以下のようになります。
コードは以下のように書きます。
import numpy as np import matplotlib.pyplot as plt def f(x,y): return x*y def true(x): return 4.0*np.exp(x**2/2.0) if __name__=="__main__": # 初期値 x0 = 0.0 y0 = 4.0 # どこまで計算するか x_end = 3.0 # 分割数 n = 100 # 刻み幅 dx = np.abs(x_end-x0)/n # データを格納する配列 x = np.zeros(n+1) y = np.zeros(n+1) y_true = np.zeros(n+1) x[0] = x0 y[0] = y0 y_true[0] = y0 # オイラー法の計算 for i in range(n): y[i+1] = y[i] + f(x[i],y[i])*dx x[i+1] = x[i] + dx y_true[i+1] = true(x[i]) # 図の作成 plt.plot(x, y, label="euler method") plt.plot(x, y_true, label="true") plt.xlabel("x") plt.ylabel("y") plt.legend() plt.show()
グラフを作成すると、以下のようなグラフができます。
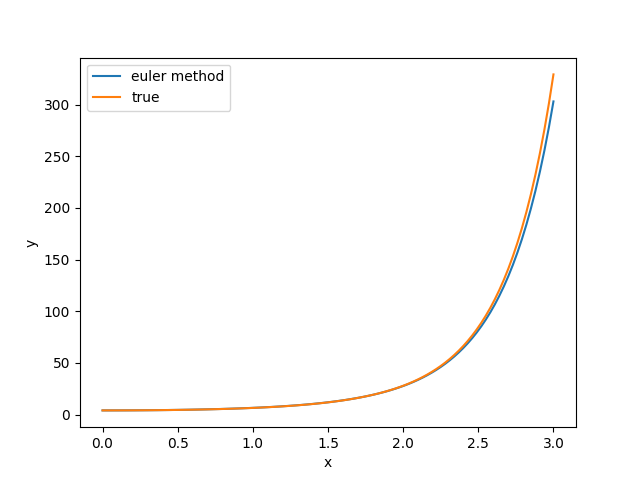
オイラー法と厳密解では、ずれがあることが確認できます。
もっと精度良く計算するには、分割数を増やすか、より精度の良い手法を用いる必要があります。