こんにちは。
今回は、二分法という非線形方程式の解法について書いていきたいと思います。
過去二回、非線形方程式の解法として、ニュートン法とセカント法について書きましたが、これらの方法は収束しないことがありますが、二分法は必ず収束する方法となります。
ニュートン法とセカント法の記事については、以下にリンクを貼りますので、興味のある方は是非ご覧ください。
c言語で非線形方程式の解法(ニュートン法) - pypy.com/
c言語で非線形方程式の解法(セカント法) - pypy.com/
それでは、書いていきます。
二分法の考え方
以下の図を用いて考えます。

まず、初期値を二点設定します。
今回は を初期値として考えます。
この時、初期値に設定する点は
となるようにします。
二分法では、この後、その二点の中点を求めます。
ここで、 の絶対値が十分に小さければそこで、計算を終了します。
絶対値が十分に小さくない場合は、 の正負を判定し、正であれば、
、負であれば、
との中点を求め、その点を次の点とします。
上図の場合、 であるので、
となります。
この計算を繰り返し行い、絶対値が小さくなったところで、計算を終了します。
二分法のc言語コード
今回は、以下の式の解を求めたいと思います。
グラフだと以下のものです。
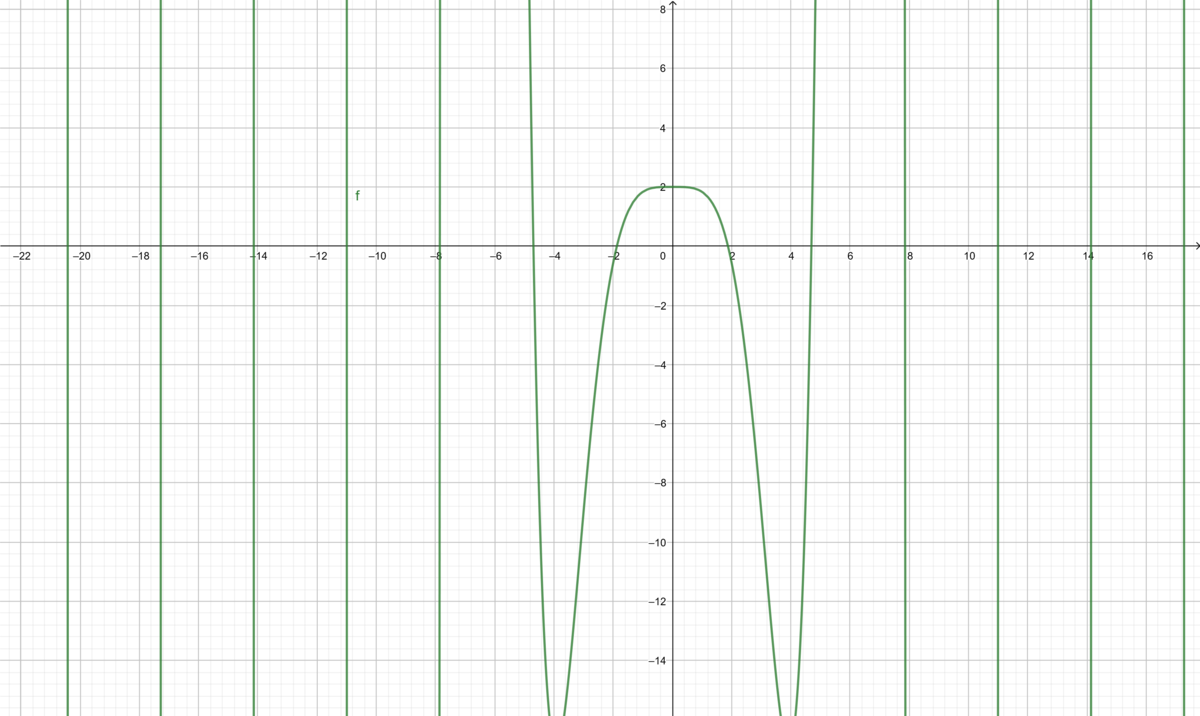
コードは以下のように書きました。
#include <stdio.h> #include <math.h> double f(double x); int main(void){ double x_start1 = 4.0; double x_start2 = 0.0; double err = 100.0; double a = x_start1; double b = x_start2; double c; while(err>0.00000001){ c = (a+b)/2.0; double fc = f(c); err = fc*fc; if(fc > 0){ b = c; } else{ a = c; } printf("%lf\n",c); } printf("result:%lf\n",c); } double f(double x){ return cos(x)*cosh(x)+1.0; }
実行結果は以下のようになります。
2.000000 1.000000 1.500000 1.750000 1.875000 1.937500 1.906250 1.890625 1.882813 1.878906 1.876953 1.875977 1.875488 1.875244 1.875122 result:1.875122
うまく解が求まっていることがわかります。
以上で終わります。