こんにちは。
今回はガウス過程回帰をpythonで書いてみたいと思います。
最近、「ガウス過程と機械学習」という本を読んで少し勉強したので、アウトプットのために書きたいなと思いました。
一応、読んだ本のURLは以下に貼っておきます。
興味のある方は読んでみると面白いかもしれません。
今回書くのは、基本的なところのみにしたいと思います。
ハイパーパラメータの最適化や処理速度についてはあまり考えないことにします。
それでは書いていきます。
ガウス過程回帰とは
簡単に説明すると、入力変数 と出力変数
があったときに、
を推定するモデルの一つとなります。
一般的な線形回帰では、
というモデルがあって、このの重み付けを行って
を求めますが、
この手法だと次元数が増えたときにとてつもない計算時間になり処理しきれなくなるので、
ガウス過程回帰ではカーネルトリックと呼ばれるような手法を使います。
カーネルトリック
かなり端折ってしまうと、ガウス過程回帰では、の分布は以下の共分散行列のみで決まります。
この要素は、xの特徴ベクトルをΦ(x)として、以下のようになります。
また、yの平均が0であるとき、さらに簡単になり、
さらに、このとき、カーネル関数と呼ばれる関数で、この要素を表すことができ、
と、表現することができる。
今回使うカーネル関数
今回使うのは、ガウスカーネルと呼ばれるものに観測ノイズを考慮した、以下のカーネル関数を使います。
使った教科書では、最もよく使われると記載されています。
今回はこれを使いますが、カーネル関数にはかなりの種類があるので、データによって使い分ける必要があります。
実際にガウス過程回帰のコードを書いていく
カーネルクラス
このクラスではカーネルを作ります。
カーネル関数を変えたい場合は、kernel_subのelementの計算を変えます。
class Kernel: def __init__(self, sita1=1.0, sita2=0.4, sita3=0.1): self.sita1 = sita1 self.sita2 = sita2 self.sita3 = sita3 # カーネルの要素を返す # とりあえず、ガウスカーネルを使う(教科書で最もよく使われると書いてある、3.26式) def kernel_sub(self,x1,x2,i=1,j=2): """ カーネルの要素を計算する :param x1: 1次のnumpy配列 :param x2: 1次のnumpy配列 :param i: x1の要素番号 :param j: x2の要素番号 :return: カーネル行列の要素 """ # ユークリッド距離 dis = np.linalg.norm(x1-x2) delta = 1 if (i == j) else 0 # カーネルの要素 element = self.sita1 * np.exp(-1.0 * dis*dis / self.sita2) + self.sita3*delta return element def kernel_make(self,x1,x2,mode=0): """ カーネルを計算する :param x1: 行列1 :param x2: 行列2 :param mode: 0:通常 1:kstarの時 :return: カーネル行列 """ # numpy配列の初期化 kernel_np = np.zeros((x1.shape[0],x2.shape[0])) # kernelの計算 if(mode==0): for i in range(x1.shape[0]): for j in range(x2.shape[0]): kernel_np[i,j] = self.kernel_sub(x1[i],x2[j],i,j) else: for i in range(x1.shape[0]): for j in range(x2.shape[0]): kernel_np[i,j] = self.kernel_sub(x1[i],x2[j]) return kernel_np
データ読み込み、前処理部分
ここでは、データの読み込みと、軽い前処理を行います。
今回は、アワビのデータを使います。
結構、回帰に使うデータセットとしては有名らしい?
データはこんな感じです。
Sex Length Diameter Height ... SWeight VWeight ShWeight NoShellRings 0 M 0.455 0.365 0.095 ... 0.2245 0.1010 0.1500 15 1 M 0.350 0.265 0.090 ... 0.0995 0.0485 0.0700 7 2 F 0.530 0.420 0.135 ... 0.2565 0.1415 0.2100 9 3 M 0.440 0.365 0.125 ... 0.2155 0.1140 0.1550 10 4 I 0.330 0.255 0.080 ... 0.0895 0.0395 0.0550 7 ... .. ... ... ... ... ... ... ... ... 4172 F 0.565 0.450 0.165 ... 0.3700 0.2390 0.2490 11 4173 M 0.590 0.440 0.135 ... 0.4390 0.2145 0.2605 10 4174 M 0.600 0.475 0.205 ... 0.5255 0.2875 0.3080 9 4175 F 0.625 0.485 0.150 ... 0.5310 0.2610 0.2960 10 4176 M 0.710 0.555 0.195 ... 0.9455 0.3765 0.4950 12
データをトレーニング用とテスト用に分けるところまで書きます。
if __name__ == '__main__': # csv読み込み(とりあえず、Pandasで) data = pd.read_csv('abalone.data', names=('Sex','Length','Diameter','Height','WWeight','SWeight','VWeight','ShWeight','NoShellRings')) print(data) # 今回はSex(文字列データ)を整数値に変換する # とりあえず、M=1,I=0,F=-1 にする data["SexInt"] = data['Sex'].apply(lambda x : 1 if x == 'M' else (0 if x=='I' else -1)) print(data) # もうSexデータは使わないので抜いておく data = data[['SexInt','Length','Diameter','Height','WWeight','SWeight','VWeight','ShWeight','NoShellRings']] # データを標準化する # そろそろNumpyベースの処理にする(Numpyのほうが速く、有効桁数も大きい) data_np = data.values #data_np = scipy.stats.zscore(data_np) print(data_np) # データをXとYに分ける X = data_np[:,0:8] Y = data_np[:,8] print(X) print(Y) # Xのデータを標準化する X_std = scipy.stats.zscore(X, axis=0) # データをtestとtrainに分ける TrainX = X_std[0:3500,:] TrainY = Y[0:3500] TestX = X_std[3500:,:] TestY = Y[3500:] print(TrainX) print(TrainY)
カーネルの作成と予測
そういえば、書き忘れていましたが、予測したい点を、出力を
として、
となります。
コードは以下の感じです。
# カーネル行列を作成 kernel = Kernel() K = kernel.kernel_make(TrainX,TrainX) print(K) # カーネルの逆行列 K_inv = np.linalg.inv(K) # テストデータの予測 k_star = kernel.kernel_make(TrainX,TestX,1) k_star2 = kernel.kernel_make(TestX,TestX) means = np.dot(k_star.T, np.dot(K_inv, TrainY)) vars = k_star2 - np.dot(k_star.T, np.dot(K_inv, k_star)) # 分散を標準偏差に変換 stds = np.sqrt(vars) means = np.round(means)
予測値はmeans、標準偏差がstdsに入っています。
今回は予測値がアワビの年齢なので、最後に四捨五入しています。
plotしてみる
最後にプロットしてみます。
プロットするのは、テストデータです。
プロットがかなり重なるので、trueと予測値を分けてプロットします。
# plot plt.xlim(0,1) #x軸範囲指定 plt.ylim(0,20) #y軸範囲指定 # 元データ plt.plot(X[3500:,3], TestY, 'x', color='green', label='correct signal') plt.show() # plot plt.xlim(0, 1) # x軸範囲指定 plt.ylim(0, 20) # y軸範囲指定 # predictデータ plt.plot(X[3500:,3], means, 'o', color='blue', label='mean by Gaussian process') #plt.plot(TestX, mean_list + 2*std_list, mean_list - 2*std_list, ',', color='red', label='2σ by Gaussian process') plt.show()
true値
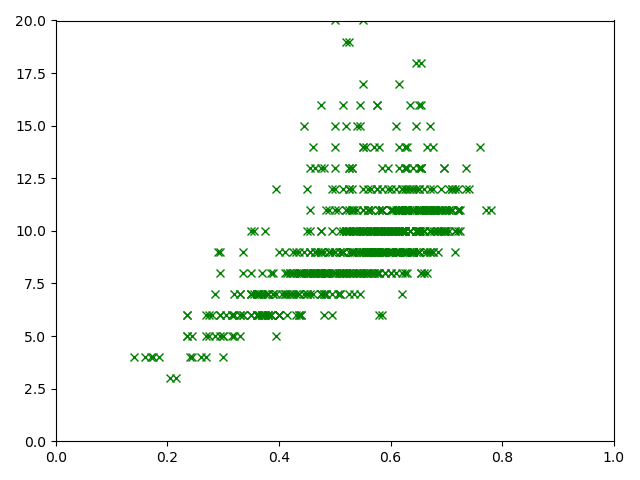
予測値
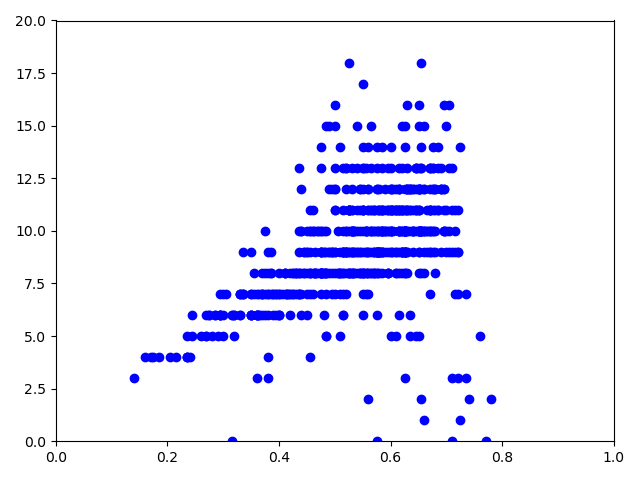
結構いい感じに予測できているのではないでしょうか。
今度はハイパーパラメータの最適化にも挑戦してみたいと思います。