pypy.com/

Python、Unity、FX自動化などを勉強しています。あと、コーラと車も好きです。そこらへんについて、たまに記事を書きます。

c言語で数値積分（台形則・台形公式）

こんにちは。

今回は、数値積分２回目ということで、台形則について書いていきたいと思います。

前回書いた長方形近似のものと、考え方がほぼ一緒なので、わかりやすいかなと思います。

前回の長方形近似のものは、以下から見ることができるので、興味のある方はご覧ください。

それでは書いていきます。

台形則の考え方

以下の図を用いて考えていきます。

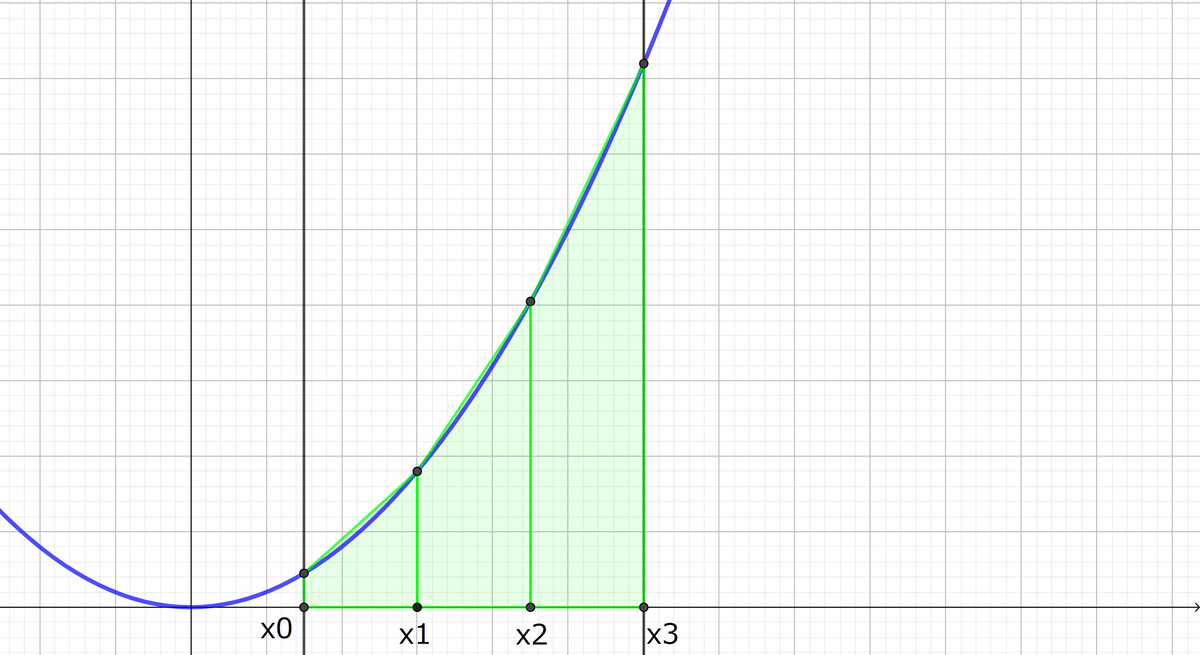
上の図の x_0 から x_3 まで積分する場合について、考えます。

台形則では、図の緑の部分のように積分する場所を台形に近似して、その面積を求めることで値を出していきます。

例えば、図の一番左側の台形の面積を S_1 とすると、

台形の面積の公式を用いて、

S_1=\frac{f(x_0)+f(x_1)}{2}(x_1-x_0)

となります。

ここで、

h=\frac{x_3-x_0}{3}

とすると、

S_1=\frac{f(x_0)+f(x_1)}{2}h

であるので、

同様に、左から二番目の台形の面積を S_2 三番目を S_3とすると、

求める積分値 S は、

S \simeq S_1+S_2+S_3=\frac{f(x_0)+f(x_1)}{2}h+\frac{f(x_1)+f(x_2)}{2}h+\frac{f(x_2)+f(x_3)}{2}h

として、求めることができます。

C言語でコードを書いてみる

今回は、前回と同様、以下の式の定積分を0.0～1.0の範囲で積分していきたいと思います。

f(x)=x^2+x+1

コードは以下のように書くことができます。

#include<stdio.h>

double func(double x);

void main(){
  // 積分範囲
  double a = 0.0;
  double b = 1.0;
  // 分割数
  double n = 10;
  double step = (b - a) / n;
  double sum = 0.0;
  for(int i = 0; i < n; i++){
    double s = ((func(a + step*i) + func(a + step*(i+1))) / 2.0) * step;
    sum = sum +s;
  }
  printf("計算結果 = %lf\n",sum);
}

double func(double x){
  return x*x + x + 1.0;
}

これを実行してみると、以下のような出力となります。

計算結果 = 1.835000

今回求めたものの厳密解が1.83333333であるので、
かなり近い値が出ていることがわかります。

前回の長方形近似で出した値の1.735に比べるとかなり近づきました。

今回は以上で終わります。

また、数値計算系の記事は書くと思うので、気になる方は見ていただけると嬉しいです。